Regletas Cuisenaire

Inventadas por el belga George Cuisenaire, estas regletas están diseñadas para trabajar las cuatro operaciones básicas, fracciones, áreas y volúmenes, ecuaciones lineales simples, sistemas de ecuaciones e incluso ecuaciones cuadráticas

1. Operaciones básicas

  • Suma:
    Vemos que la longitud de la regleta de color púrpura coincide con la longitud de las dos regletas de abajo. Cómo la longitud de la regleta color púrpura es 4 cm, 1+3 es igual a 4.


     
  • Resta:
    Suponga que se desea hallar la diferencia de 8-5 usando las regletas. La regleta de menor longitud se pone encima.



    Después de hacer varias pruebas, vemos que la longitud de la regleta verde claro coincide con la parte sobrante de la regleta mayor.
    Como la regleta verde claro mide 3 cm y su longitud es igual a la parte sobrante, 8-5 es igual a 3.


     
  • Multiplicación:
    Suponga que se pide el resultado 3 x 2 usando las regletas:



    El primer factor, que es el 3, está indicando cuántas regletas rojas se deben poner como se ve en la imagen. En este caso se deben poner tres regletas rojas.



    Después de probar con distintas regletas, la regleta verde oscura de longitud 6 cm coincide con la longitud que forman las regletas de abajo. Esto quiere decir que 3 x 2 es igual a 6.
  • División:
    Suponga que se pide el resultado 10/2 usando las regletas:
    Para dividir 10 entre 2, se debe proceder de la siguiente manera:
    Debajo de la regleta naranja se ubican regletas rojas hasta que estas cubran exactamente su longitud. Luego se cuentan las regletas rojas siendo el número de estas el resultado de dividir diez entre dos.



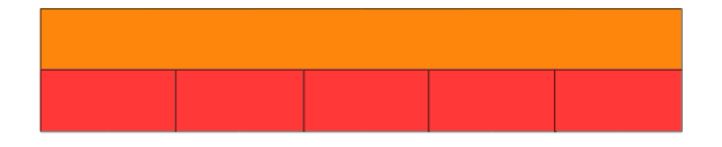
    Hasta aquí hemos visto divisiones con residuo igual a cero.
    Vamos a ver ahora divisiones con residuo diferente de cero:
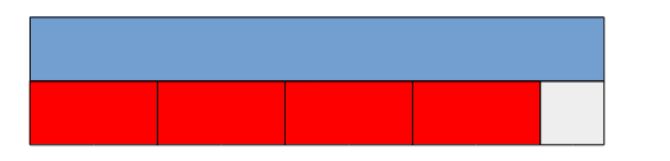
    Dividir 9/2, es decir, 9 entre 2:
    Debajo de la regleta azul se colocan regletas rojas hasta que estas completen exactamente su longitud. Vemos que no completan exactamente su longitud y queda un espacio. La regleta que completa su longitud es la blanca, luego 9 entre dos es igual a 4 y su residuo es 1.


     

2. Fracciones:

Una regleta blanca representa la fracción 1/10 , dos regletas serían 2/10 , y así sucesivamente.

Para calcular la suma de 1/2+1/5 se juntan la regleta amarilla con la regleta roja y se colocan debajo de las 10 regletas blancas. Vemos que la suma de la regleta amarilla con la regleta roja equivale a 7/10 al completar completamente con 7 regletas blancas.
 


 

Regleta              Partes en que se divide Color de la regleta que representa cada parte Fracción que representa esa regleta
Naranja 2 Amarilla 1/2
Naranja 5 Roja 1/5
Naranja 10 Blanca 1/10