La biblioteca de mi centro usada como aula de matemáticas

Introducción

En la Tercera Conferencia Internacional sobre Investigación y Racionalización del Mercado del Libro, celebrada en Berlín en noviembre de 1966, se discutió por vez primera la necesidad y la viabilidad de un sistema numérico internacional para los libros.
El sistema que cumplía tal requisito, y que pasó a conocerse como el International Standard Book Number (ISBN) (Sistema Internacional de Numeración de Libros) se desarrolló a partir del método de numeración de libros introducido por J. Whitaker & Sons Ltd. en el Reino Unido en 1967, y en los Estados Unidos, por la compañía R. R. Bowker, en 1968.

Ventajas del ISBN

El ISBN es un identificador internacional único para publicaciones monográficas; el número de diez dígitos que se inscribe en él sustituye a los largos registros de descripción bibliográfica. Se ahorran tiempo y gastos de personal, y se evitan los errores de copia.
El ISBN permite la compilación y actualización de directorios sobre ventas de libros, como por ejemplo el de Libros Impresos. Se puede encontrar fácilmente la información sobre los libros disponibles.
El pedido y distribución de libros se hace fundamentalmente a través del ISBN; es un método rápido y eficaz.
El ISBN puede ser leído por las máquinas gracias al código de barras Bookland Ean de 13 dígitos. Es un sistema rápido que evita que se produzcan errores.
El ISBN es necesario para el funcionamiento de los terminales de punto de venta electrónicos de las librerías.
La gestión de derechos se realiza fundamentalmente sobre la base del ISBN.
Las cifras de ventas se controlan gracias al ISBN.
Las bibliotecas se benefician de la catalogación de copias que facilita el ISBN.
El derecho de préstamo nacional de determinados países se basa en el ISBN.

Utilizaremos el concepto de ISBN para conseguir el objetivo didáctico de explorar distintas maneras de proceder y obtener posibles soluciones utilizando como aula la biblioteca del centro y alineando saberes básicos numéricos y estocásticos, así como socioafectivos.

Justificación

Siguiendo las Iinstrucciones de la Viceconsejería de Desarrollo Educativo y Formación Profesional sobre las medidas para el fomento del razonamiento matemático a través del planteamiento y la resolución de retos y problemas en Educación Infantil, Educación Primaria y Educación Secundaria Obligatoria, una de las principales formas de aprender Matemáticas es resolver problemas. En el Decreto 102/2023 de 9 de mayo, por el que se establece la ordenación y el currículo de la etapa de Educación Secundaria Obligatoria en la Comunidad Autónoma de Andalucía, el razonamiento matemático está presente, con especial atención a la iniciación temprana en habilidades numéricas básicas, la manipulación de objetos y la comprobación de fenómenos. Con la Unidad Didáctica de título 'La biblioteca de mi centro usada como aula de matemáticas' intentaremos que el alumnado adquiera los siguientes objetivos de etapa usando los principios pedagógicos abajo citados:

Objetivos de la etapa

Desarrollar y consolidar hábitos de disciplina, estudio y trabajo individual y en equipo como condición necesaria para una realización eficaz de las tareas del aprendizaje y como medio de desarrollo personal.
Desarrollar destrezas básicas en la utilización de las fuentes de información para, con sentido crítico, adquirir nuevos conocimientos. Desarrollar las competencias tecnológicas básicas y avanzar en una reflexión ética sobre su funcionamiento y utilización.

Principios pedagógicos

Lectura.
Uso de TIC.
Desarrollo sostenible y el medio ambiente.
DUA.
Inteligencia emocional.
Patrimonio cultural andaluz.
Resolución pacífica de conflictos.
Realización de proyectos significativos para el alumnado.
Actividades para profundizar en las habilidades y métodos de recopilación, de sistematización y de presentación de la información, para aplicar procesos de análisis, de observación y de experimentación, mejorando habilidades de cálculo y desarrollando la capacidad de resolución de problemas, fortaleciendo así habilidades y destrezas de razonamiento matemático.

Producto final

Infografía de biblioteca. Haciendo uso del máximo común divisor y del mínimo común múltiplo, diseñarán un mueble para la biblioteca para colecciones de 2, 3, 5 y 7 libros. Con las regletas Cuisenaire o mediante medios digitales harán una infografía de cómo quedarían dichas colecciones en el mueble y cómo sería la ficha del libro para poder almacenarlo.

Concreción curricular

Competencia específica 1

Interpretar, modelizar y resolver problemas de la vida cotidiana y propios de las matemáticas, aplicando diferentes estrategias y formas de razonamiento, para explorar distintas maneras de proceder y obtener posibles soluciones. ( El desarrollo de esta competencia conlleva aplicar el conocimiento matemático que el alumnado posee en el contexto de la resolución de problemas. Para ello, es necesario proporcionar herramientas de interpretación y modelización (diagramas, expresiones simbólicas, gráficas, etc.) técnicas y estrategias de resolución de problemas como la analogía con otros problemas, la estimación, el ensayo y error, la resolución de manera inversa (ir hacia atrás), el tanteo, descomposición en problemas más sencillos o la búsqueda de patrones, que les permitan tomar decisiones, anticipar la respuesta, asumir riesgos y aceptar el error como parte del proceso.

Criterios de evaluación

Se inicia en la interpretación de problemas matemáticos sencillos, reconociendo los datos dados, estableciendo, de manera básica, las relaciones entre ellos y comprendiendo las preguntas formuladas.
Aplicar, en problemas de contextos cercanos de la vida cotidiana, herramientas y estrategias apropiadas, como pueden ser la descomposición en problemas más sencillos, el tanteo, el ensayo y error o la búsqueda de patrones, que contribuyan a la resolución de problemas de su entorno más cercano.
Obtener las soluciones matemáticas en problemas de contextos cercanos de la vida cotidiana, activando los conocimientos necesarios, aceptando el error como parte del proceso.

Saberes básicos a utilizar

Cuando evaluemos el 1: A21 (Notación científica) , A23 (Cantidades en contextos de la vida cotidiana, E12 (Análisis e interpretación de tablas estadísticas).
Cuando evaluemos el 2: A31 (Cálculo mental) , B12 (Elección de unidades).
Cuando evaluemos el 3: A22 (Estimaciones) , A34 (Operaciones ), F13 (Error como aprendizaje).

Descriptores operativos

STEM 1 a 4: Resolución de problemas con métodos inductivos y deductivos, experimentos sencillos, proyectos con prototipos, estudio de casos vinculado a experimentos con transmisión mediante elementos digitales y gráficos estadísticos de conocimiento científico.
CD2: Gestión del entorno personal de aprendizaje y búsqueda de información.
CPSAA5: Autoevaluación y Coevaluación y toma de conciencia de errores cometidos.
CE3: Creación de modelo innovador para aportar soluciones en un proyecto en equipo.
CCEC4: Creación de producto artístico y cultural.

Secuenciación didáctica

Fase 1: Motivación (1 sesión de 1 hora)

Fomento a la lectura (en pdf tenemos el siguiente texto en cursiva)

Antiguamente el ISBN consistía en un número de 10 dígitos. El algoritmo de verificación de los ISBN de 10 dígitos es el siguiente:

Se multiplican los dígitos de izquierda a derecha por 10, 9, 8, 7, 6, 5, 4, 3, 2 y 1 respectivamente.
Se suman los productos anteriores.
El resultado tiene que ser múltiplo de 11. Si no es así, el ISBN es incorrecto.

Si queremos conocer el Dígito de Control, realizamos esas mismas operaciones, sin el último producto, de modo que el número resultante, en principio, no es múltiplo de 11. El dígito de control será la cantidad necesaria hasta el siguiente múltiplo. En el caso de que sí fuera múltiplo de 11, el Dígito de Control sería 0, y si la cantidad necesaria es 10, ese dígito es una X.

El nuevo ISBN tendrá 13 dígitos: el prefijo de 3 dígitos que identifica el sector del libro (actualmente, «978»), seguido del número central de 9 dígitos, y el dígito de comprobación, que valida la integridad interna de todo el número. Como tal, será idéntico al código EAN «Bookland» de 13 dígitos que ya aparece en el código de barras impreso de la cubierta posterior del libro.

Los números ISBN-10 e ISBN-13 se dividen en cuatro o cinco elementos, respectivamente. Tres de los elementos son de longitud variable; el o los dos elementos restantes son de longitud fija. Las cinco partes suelen estar separadas por guiones o espacios. A continuación se ofrece una breve descripción de cada elemento:

Los ISBN de 13 dígitos comienzan con el prefijo 978 o 979.
El identificador de grupo identifica el grupo de países que comparten el idioma. Tiene una longitud de entre uno y cinco dígitos.
El identificador del editor varía en longitud y lo asigna la agencia nacional del ISBN.
El identificador del título también varía en longitud y es seleccionado por el editor.
El último carácter se denomina dígito de control y se calcula mediante un algoritmo de suma de comprobación. Un dígito de control de ISBN-10 puede ser un número del 0 al 9 o la letra X (número romano para 10), mientras que un dígito de control de ISBN-13 varía del 0 al 9. Los caracteres permitidos son diferentes porque los dos tipos de ISBN utilizan algoritmos de suma de comprobación diferentes.

Suma de comprobación del ISBN-13

Un dígito de control ISBN-13 varía de 0 a 9 y se calcula utilizando pasos similares.

Multiplica cada uno de los primeros 12 dígitos por 1 o 3, alternando mientras te mueves de izquierda a derecha, y suma los resultados.
Divida la suma por 10.
Resta el resto (no el cociente) de 10.
Si el resultado es 10, utilice el número 0.

Por ejemplo, el dígito de control del ISBN-13978-0-596-52068-? Se calcula de la siguiente manera:

Las casas editoriales y las imprentas que utilicen un programa propio para crear códigos de barras deberán asegurarse de que se adapta a este nuevo requisito, y deberán asegurarse de que sus proveedores de soportes de filmación o códigos de barras electrónicos interpreten correctamente este requisito.

Actividad M1: Haremos una lectura individual del pdf anterior (o escucha en podcast en caso de alumnos con déficit visual) y contestaremos a las siguientes preguntas:

¿Cómo sabes que el EAN (Código de barras) de arriba pertenece a un libro?
¿Es correcto el número 9781873671009 como número ISBN en Europa?

Si para la editorial 9916 se le reservan 3 dígitos para sus títulos (Cómo por ejemplo el libro 901) ¿Cuántos libros distintos, como máximo, podrá tener esa editorial?
Si en España se han reservado 4 dígitos para las editoriales, ¿cuántas editoriales, como máximo, podrá tener España?
Dígito de control en ISBN de 10 dígitos (Módulo 11).

Ejemplo:

¿Recuerdas cuál era la jerarquía en las operaciones con números naturales ([], (),*,/,+,-)?
¿Recuerdas la regla para saber si un número natural era múltiplo de 11?
¿Sabrías decirme otras tres reglas de distintos divisores (2,3,5,7,¿)?

Una vez hechas las actividades arriba indicadas, podremos hacer una evaluación inicial sobre los conocimientos que poseen de potencias de base 10, múltiplos y divisores, orden en las operaciones con números naturales mediante observación directa.

Les explicaremos las rúbricas de los Criterios de evaluación (Rúbrica holística de los criterios 1.1, 1.2 y 1.3. ), así como el Producto final Infografía, con los libros de la Biblioteca, ordenación y códigos ISBN empleados en cada libro. Resumen de un capítulo del libro elegido y entrega del porfolio.

Fase 2: Activación (1 sesión de 1 hora)

Actividad A1: ¿Recuerdas lo que sabes de cursos anteriores de múltiplos y divisores? Múltiplos y divisores.

Múltiplos de un número.
Divisores de un número.
Números primos y números compuestos.
Reglas de los divisores.
Divisor 2. Divisor 3. Divisor 5. Divisor 7. Divisor 11.
Factorización de un número.

Jugamos con el laboratorio digital (también disponemos de material manipulativo para atención a la diversidad) donde introducimos los conceptos ya estudiados de MCD y mcm.

Fase 3. Exploración (1 sesión de 1 hora)

Actividad E1: Acertijo

Cada año un rey aficionado a las matemáticas recibe de sus 10 nobles un saco con monedas de oro. Cada moneda pesa 10 gramos. Un año un noble decide estafar al rey dándole monedas que pesan 9 gramos.

El espía del rey le advierte que alguien le está engañando y el rey haciendo una sola pesada en una balanza a los sacos descubre quién le ha estado engañando.

¿Cómo lo ha hecho?

Solución:

El rey pesó una moneda del primer noble, dos monedas del segundo, tres monedas del tercer, ¿, 9 monedas del noveno y 10 monedas del décimo. Si no hubiese habido intentos de estafa la pesada daría 550 gramos:

10*[1+2+3+4+5+6+7+8+9+10] = 10*[(10)+(1+9)+(2+8)+(3+7)+(4+6)+5)] =550 gramos
Si pesa 549=550-1 el estafador es el primer noble.
Si pesa 548=550-2 el estafador es el segundo noble.
...
Si pesa 541=550-9 el estafador es el noveno noble.
Si pesa 540=550-10 el estafador es el décimo noble.

Actividad E2: Creación de la Biblioteca de cada grupo

Si tenemos un mueble de Biblioteca con 3 baldas como el de la figura y entre balda y balda hay 40 cm, el ancho de la balda es 35 cm y la longitud total del mueble son 200 cm:

¿Cuántos huecos diferentes hay por puerta?
¿Cuántos huecos diferentes hay en el mueble?
¿Podría decir aproximadamente cuántos libros de gran formato (2 cm *30cm*25cm) hay en la biblioteca?
¿Para esa cantidad de libros cuántos dígitos necesitarías en un código interno propio que tiene 15 colecciones distintas de gran formato y cada colección dispone de entre 8 y 24 títulos distintos?
Si bastase con 4 dígitos, podríamos poner un dígito más de control para garantizar que el número es correcto?

Fase 4: Estructuración (8 sesiones de 1 hora)

Saberes implicados y actividades

A21 (Notación científica). Explicaciones de números grandes y pequeños como potencias de base 10 en notación científica.

Actividad 1: Apilamos libros hasta llegar a la Luna (distancia Tierra-Luna 384,400 km ). Si cada libro mide 5 cm de ancho, ¿Cuántos libros hacen falta para llegar a la Luna?
Actividad 2: Si en el sistema internacional de unidades para la longitud la unidad de medida es el metro, ¿podrías convertir la distancia Tierra-Luna a metros y expresarla en notación científica?

A23 (Cantidades en contextos de la vida cotidiana).

Actividad 3: ¿Cuántos libros lees al año?¿Cuántos libros leeremos en el instituto al año si somos 880 alumnos, 105 docentes y 25 no docentes ni alumnos? Si en Andalucía hay unos 4000 IES, ¿cuántos libros se leen al año?

E12 (Análisis e interpretación de tablas estadísticas)

Actividad 4: Cada equipo debe interpretar las tablas estadísticas proporcionadas por la Junta de Andalucía: https://juntadeandalucia.es/sites/default/files/2024-06/INFORME%202023.pdf
- Debe encontrar el número de visitantes de biblioteca de su provincia y estimar cuántos libros se han leído ese año en su provincia, expresando el resultado en notación científica, aproximando el resultado por redondeo al alza con dos cifras decimales.
- Utilizando el diagrama de sectores, se debe estimar el número de libros leídos en toda Andalucía.

A31 (Cálculo mental). Gauss

Actividad 5: En la fase de exploración hicimos las siguientes operaciones:
- 10*[1+2+3+4+5+6+7+8+9+10] = 10*[(10)+(1+9)+(2+8)+(3+7)+(4+6)+5)] =550 gramos.
- ¿Por qué crees que se agruparon así los números?

Vamos a leer la Anécdota de Gauss que viene en un libro conmemorativo sobre la vida de Gauss («Gauss zum Gedächtnis«) que se publicó en 1856, justo un año después de la muerte de Gauss, cuyo autor fue Wolfgang Sartorius, el barón von Waltershausen, profesor de mineralogía y geología en la Universidad de Göttingen, donde Gauss desarrolló su carrera académica.

La elegía a Gauss de Sartorius rebosa cariño y admiración. De la infancia de Gauss, Sartorius nos relata que aprendió a leer él solo (autodidacta) y que a los tres años le corrigió un error aritmético a su padre. Gauss fue escolarizado de forma temprana en la ciudad de Braunschweig, cerca de Hanover. Sartorius nos cuenta la historia de la famosa anécdota como sigue:

En 1784, tras su séptimo cumpleaños, el pequeño entró en una escuela pública de educación primaria donde las clases las impartía un profesor llamado Büttner. La escuela estaba ubicada en una habitación sombría, de techo bajo, suelo desigual, ¿ donde cerca de un centenar de pupilos de Büttner iban y venían. El profesor imponía una disciplina rígida y nadie podía llevarle la contraria. En esta escuela, que seguía el patrón de la Edad Media, Gauss llevaba dos años como alumno sin provocar ningún incidente reseñable.

El primer día que Gauss asistió a la clase de Aritmética, en la que había niños de hasta 15 años, ocurrió un incidente que Gauss solía contar ya anciano para el deleite de sus contertulios. Cuando el profesor proponía un problema, el alumno que acababa el primero tenía que llevar su pizarrita hasta la mesa del profesor. El segundo que lo lograra colocaba la suya encima, y así sucesivamente. El primer día que el joven Gauss entró en clase, el profesor Büttner, a viva voz, estaba dictando un problema de aritmética para sus alumnos. Justo al acabar de dictar el problema, Gauss colocó su pizarrita sobre la mesa del profesor, quien con absoluta seguridad afirmó: «Debe estar mal.» Mientras, el resto de los alumnos continuaron con su tarea (contando, multiplicando, y sumando). Büttner recorría la clase observando a sus alumnos con una mirada irónica, casi compasiva, hacia sus alumnos. Sólo un niño estaba sentado, callado, con su tarea ya finalizada, consciente de que la había resuelto correctamente y que su resultado era el único posible.

Al final de la clase, el profesor dio por acabado el examen y volvió las pizarras hacia arriba. La primera, la del joven Gauss, sólo contenía un número. Cuando Büttner lo leyó, para su sorpresa y la de todos los presentes, resultó que la respuesta del joven Gauss era correcta. Muchos de sus compañeros, sin embargo, habían obtenido una respuesta errónea.

Creemos que el problema de aritmética que pidieron era sumar los números del 1 al 100.

Se cuenta que Gauss hizo esta suma en poco más de 10 segundos cuando tenía 4 años, usó el siguiente maravilloso truco: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101¿, luego la suma es 101 x 100 / 2 = 5.050.

Hay otras agrupaciones que sirven para reforzar nuestro cálculo mental:

Esta imagen está tomada de https://www.recursosep.com/

B12 (Elección de unidades).

Actividad 6: Tamaño de un libro
- Ancho de la hoja de un libro.
- Tamaño de la balda de la biblioteca.
- Área del suelo de la biblioteca.
- Área de la hoja de un libro.
- Utiliza el material manipulativo de regletas de Cuisenaire y monta tu biblioteca, indicando en las unidades que creas más adecuadas las dimensiones de cada parte de la biblioteca.

A22 (Estimaciones).

Actividad 7: Utiliza el material manipulativo de regletas de Cuisenaire y monta tu biblioteca, indicando en las unidades que creas más adecuadas las dimensiones de cada parte de la biblioteca.
- Una vez hecho, vamos a estimar cuánto plástico tendremos que comprar para forrar los libros, así cómo cuál será la superficie total a barnizar para la biblioteca.

A34 (Operaciones).

Actividad 8: En el PORFOLIO que se entrega deben estar todas las operaciones realizadas para obtener la solución a todas las cuestiones planteadas.

F13 (Error como aprendizaje).

No importa el hecho de fallar, si no que deben ver el error como una oportunidad de aprendizaje.

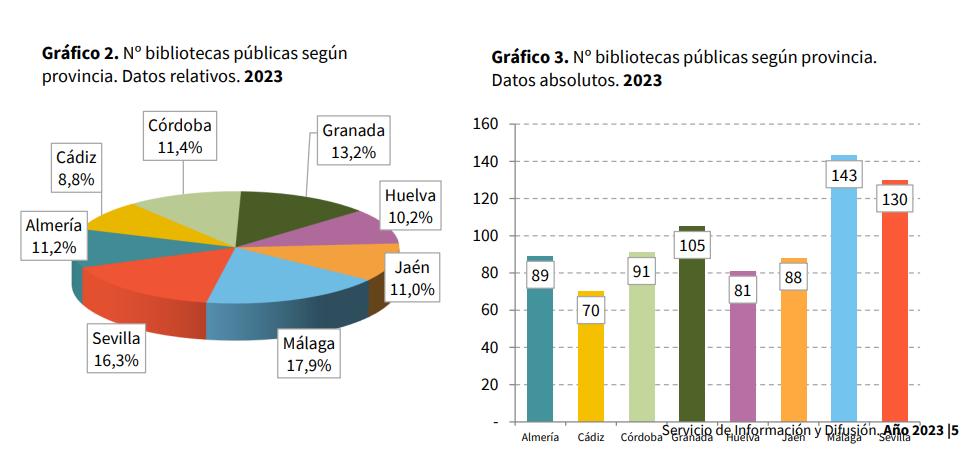
Actividad 9: Comparar el gráfico 3 ¿Nº bibliotecas públicas según provincia¿ con el gráfico 10 visto anteriormente de ¿N.º visitantes a bibliotecas públicas según provincias¿. ¿Podrías sacar algún patrón que relacione ambos gráficos?

Fase 5: Aplicación (1 sesión de 1 hora)

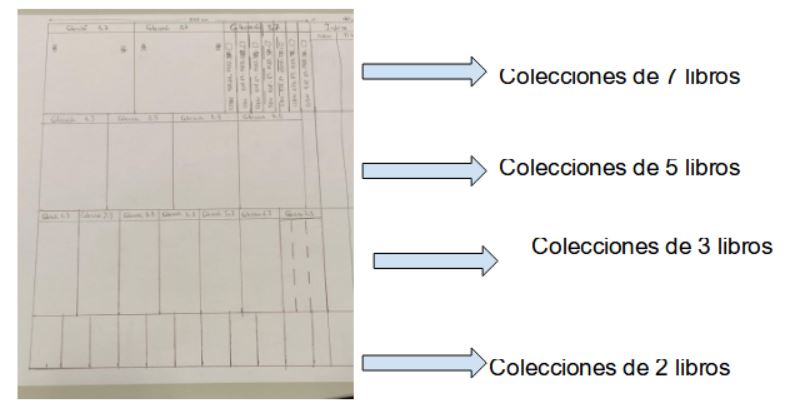
Fase 6: Conclusión/Evaluación (2 sesiones de 1 hora)

En esta fase expondrán su infografía, entregarán el porfolio y se coevaluarán mediante corubrics.

Atención a la diversidad

Principios DUA

Pautas DUA

Principio I (Múltiples formas de representación)

1. Percepción:

Alternativas a la información escrita (auditiva)

2.Lenguaje,expresiones matemáticas y símbolos:

Ilustrar las ideas principales a través de múltiples medios.

3. Comprensión:

Activar los conocimientos previos.

Principio II (Múltiples formas de acción y expresión)

4. Interacción física:

Materiales manipulativos y laboratorios digitales.

5. Expresión y comunicación:

Se permite distintos medios (digitales y analógicos para exponer la infografía)

6. Funciones ejecutivas:

Metas guiadas y apoyo en la planificación de la tarea.

Principio III (Múltiples formas
de implicación)

7. Captar interés:

Optimizamos la elección individual de cada biblioteca de grupo para que la sientan como suya.

8. Mantener el esfuerzo y la persistencia:

Rúbrica de evaluación con pautas para conseguir los objetivos en cada actividad.

9. Autoimplicación:

Desarrollo de la a autoevaluación y reflexión con CoRubrics

Medidas Generales

Equipos de trabajo heterogéneos, con tutoría entre iguales.

Evaluación

Rúbrica holística

Criterio	N1[1,3)	N2[4,5)	N3[5,7)	N4 [7,9)	N5 [9,10]
1.1	No se inicia en la interpretación de problemas matemáticos sencillos, ni reconoce los datos dados, ni establece, de manera básica, las relaciones entre ellos ni comprende las preguntas formuladas.	Le cuesta iniciarse en la interpretación de problemas matemáticos sencillos, así como reconocer los datos dados, y establecer, de manera básica, las relaciones entre ellos. También le cuesta comprender las preguntas formuladas.	Se inicia en la interpretación de problemas matemáticos sencillos, reconociendo algunas veces los datos dados, estableciendo, de manera básica, la mayoría de las veces las relaciones entre ellos y comprendiendo en algunas ocasiones las preguntas formuladas.	Se inicia en la interpretación de problemas matemáticos sencillos, reconociendo usualmente los datos dados, estableciendo, de manera básica, la mayoría de las veces las relaciones entre ellos y comprendiendo casi siempre las preguntas formuladas.	Se inicia en la interpretación de problemas matemáticos sencillos, reconociendo los datos dados, estableciendo, de manera básica, las relaciones entre ellos y comprendiendo las preguntas formuladas.
1.2	No aplica, en problemas de contextos cercanos de la vida cotidiana, herramientas y estrategias apropiadas, como pueden ser la descomposición en problemas más sencillos, el tanteo, el ensayo y error o la búsqueda de patrones, que contribuyan a la resolución de problemas de su entorno más cercano.	Le cuesta aplicar, en cualquiera de los problemas de contextos cercanos de la vida cotidiana, herramientas y estrategias apropiadas, como pueden ser la descomposición en problemas más sencillos, el tanteo, el ensayo y error o la búsqueda de patrones, que contribuyan a la resolución de esos problemas de su entorno más cercano.	Aplica, en algunos problemas de contextos cercanos de la vida cotidiana, herramientas y estrategias apropiadas, como pueden ser la descomposición en problemas más sencillos, el tanteo, el ensayo y error o la búsqueda de patrones, que contribuyan a la resolución de esos problemas de su entorno más cercano.	Aplica, en la mayoría de problemas de contextos cercanos de la vida cotidiana, herramientas y estrategias apropiadas, como pueden ser la descomposición en problemas más sencillos, el tanteo, el ensayo y error o la búsqueda de patrones, que contribuyan a la resolución de esos problemas de su entorno más cercano.	Aplica, en problemas de contextos cercanos de la vida cotidiana, herramientas y estrategias apropiadas, como pueden ser la descomposición en problemas más sencillos, el tanteo, el ensayo y error o la búsqueda de patrones, que contribuyan a la resolución de problemas de su entorno más cercano.
1.3	No obtiene las soluciones matemáticas en problemas de contextos cercanos de la vida cotidiana, ni activa los conocimientos necesarios, ni acepta el error como parte del proceso	Le cuesta obtener las soluciones matemáticas en problemas de contextos cercanos de la vida cotidiana, así como activar los conocimientos necesarios, empezando a aceptar el error como parte del proceso.	Algunas veces obtiene las soluciones matemáticas en problemas de contextos cercanos de la vida cotidiana, activando los conocimientos necesarios, aceptando el error como parte del proceso.	Usualmente obtiene las soluciones matemáticas en la mayoría de los problemas de contextos cercanos de la vida cotidiana, activando los conocimientos necesarios, aceptando el error como parte del proceso.	Obtiene las soluciones matemáticas en problemas de contextos cercanos de la vida cotidiana, activando los conocimientos necesarios, aceptando el error como parte del proceso.

Rúbrica holística

Enlace a Corubrics para coevaluación

	N1	N2	N3	N4	N5
	1	2	3	4	5
Actividad 1	No se inicia en la interpretación de problemas matemáticos	Le cuesta reconocer los datos necesarios	Reconoce los datos necesarios	Reconoce los datos necesarios	Reconoce los datos necesarios
Actividad 2	No establece, de manera básica,	No comprende el concepto de	Reconoce los datos necesarios	Reconoce los datos necesarios	Reconoce los datos necesarios
Actividad 3	No se inicia en la interpretación	Le cuesta iniciarse en la interpretación	Se inicia en la interpretación	Se inicia en la interpretación	Se inicia en la interpretación

Método de calificación

Se obtiene en cada actividad de la 1 a la 9, así como en la actividad de aplicación, una calificación de los criterios implicados según la rúbrica holística proporcionada por la Consejería. Se hará la media aritmética de las calificaciones de cada actividad (se rellenan los campos en blanco) para obtener la calificación de cada criterio. Una vez conseguida dicha calificación se obtiene una valoración de la competencia específica 1 a través de la media aritmética de las calificaciones de los criterios evaluados:

Actividad	Criterio 1.1	Criterio 1.2	Criterio 1.3
1
2
3
4
5
6
7
8
9
Aplicación
Nota media
Valoración cuantitativa / cualitativa CoEs1

Evaluación de la Unidad Didáctica

No podemos olvidar, para finalizar, que la evaluación no será solo de los niveles de aprendizaje, sino también del desarrollo del proceso de enseñanza y, por tanto, debemos realizar una autoevaluación de las acciones docentes y de los procesos seguidos, y reflejar los posibles cambios que será necesario implementar con base en indicadores previamente fijados y que aconsejen un seguimiento por parte de los equipos de coordinación docente implicados.

Evaluación del diseño de la situación de aprendizaje

Adecuación de la secuencia de actividades para el desarrollo de la competencia específica.
Idoneidad de las estrategias metodológicas y de los recursos empleados.
Pertinencia de la organización de los espacios, la temporalización de las actividades y el agrupamiento del alumnado.
Coherencia con los principios del Diseño Universal para el Aprendizaje.

Evaluación de la implementación de la situación de aprendizaje

Grado de cumplimiento de la temporalización.
Ambiente de cooperación, diálogo y aprendizaje generado en el aula.
Aplicación de los criterios e instrumentos de evaluación.
Eficacia de las medidas de individualización de la enseñanza.

Propuestas de mejora

En el diseño de la situación de aprendizaje.
En el desarrollo de la situación de aprendizaje.

Bibliografía y webgrafía

Nodo: sv0665:8080